Atomic Structure
The ancient Greek philosophers Leucippus and Democritus believed that atoms existed, but they had no idea as to their nature. Centuries later, in 1803, the English chemist John Dalton, guided by the experimental fact that chemical elements cannot be decomposed chemically, was led to formulate his atomic theory. Dalton's atomic theory was based on the assumption that atoms are tiny indivisible entities, with each chemical element consisting of its own characteristic atoms. ✶
✶ See Atoms article for further discussion of Dalton's atomic theory.
Modern View of the Atom
The atom is now known to consist of three primary particles: protons, neutrons, and electrons, which make up the atoms of all matter. A series of experimental facts established the validity of the model. Radioactivity played an important part. Marie Curie suggested, in 1899, that when atoms disintegrate, they contradict Dalton's idea that atoms are indivisible. There must then be something smaller than the atom (subatomic particles) of which atoms were composed.
Long before that, Michael Faraday's electrolysis experiments and laws suggested that, just as an atom is the fundamental particle of an element, a fundamental particle for electricity must exist. The "particle" of electricity was given the name electron. Experiments with cathode-ray tubes, conducted by the British physicist Joseph John Thomson, proved the existence of the electron and obtained the charge-to-mass ratio for it. The experiments suggested that electrons are present in all kinds of matter and that they presumably exist in all atoms of all elements. Efforts were then turned to measuring the charge on the electron, and these were eventually successful by the American physicist Robert Andrews Millikan through the famous oil drop experiment.
The study of the so-called canal rays by the German physicist Eugen Goldstein, observed in a special cathode-ray tube with a perforated cathode, let to the recognition in 1902 that these rays were positively charged particles ( protons ). Finally, years later in 1932 the British physicist James Chadwick discovered another particle in the nucleus that had no charge, and for this reason was named neutron.
GEORGE STONEY (1826–1911)
As a physical chemist, George Stoney made significant contributions to our understanding of molecular motion. However, this Irish scientist is better known for assigning a name to negative atomic charges, electrons, while addressing the Royal Society of Dublin in 1891.
—Valerie Borek
Joseph John Thomson had supposed that an atom was a uniform sphere of positively charged matter within which electrons were circulating (the "plum-pudding" model). Then, around the year 1910, Ernest Ruthorford (who had discovered earlier that alpha rays consisted of positively charged particles having the mass of helium atoms) was led to the following model for the atom: Protons and neutrons exist in a very small nucleus, which means that the tiny nucleus contains all the positive charge and most of the mass of the atom, while negatively charged electrons surround the nucleus and occupy most of the volume of the atom.
In formulating his model, Rutherford was assisted by Hans Geiger and Ernest Marsden, who found that when alpha particles hit a thin gold foil, almost all passed straight through, but very few (only 1 in 20,000) were deflected at large angles, with some coming straight back. Rutherford remarked later that it was as if you fired a 15-inch artillery shell at a sheet of paper and it bounced back and hit you. The deflected particles suggested that the atom has a very tiny nucleus that is extremely dense and positive in charge.
Also working with Rutherford was Henry G. J. Moseley who, in 1913, performed an important experiment. When various metals were bombarded with electrons in a cathode-ray tube, they emitted X rays, the wavelengths of which were related to the nuclear charge of the metal atoms. This led to the law of chemical periodicity, which provided refinement of the periodic table introduced by Mendeleev in 1869. According to this law, all atoms of an element have the same number of protons in the nucleus. It is called the atomic number and is given the symbol Z. Hydrogen is the simplest element and has Z = 1.
Bohr Model of the Atom
Through Rutherford's work it was known that that electrons are arranged in the space surrounding the atomic nucleus. A planetary model of the atom, with the electrons moving in circular orbits around the nucleus seemed an acceptable model. However, such a "dynamic model" violated the laws of classical electrodynamics, according to which a charged particle, such as an electron, moving in the positive electric field of the nucleus, should lose energy by radiation and eventually spiral into the nucleus.
To solve this contradiction, in 1913, the Danish physicist Neils Bohr (then studying under Rutherford) postulated that the electron orbiting the nucleus could move only in certain orbits, having in each a certain "quantized" energy. It turns out that the colors in fireworks would help prove him right.
Atomic Spectra
The colorful lights of fireworks are emitted by "excited" atoms; that is, by atoms that have absorbed extra energy. Light consists of electromagnetic waves, each (monochromatic) color with a characteristic wavelength λ and frequency v. Frequency is related to energy E through the famous Planck equation, E = hν , where h is Planck's constant (6.6256 x 10 −34 J s). Note that white light, such as sunlight, is a mixture of light of all colors, so it does not have a characteristic wavelength. For this reason we say that white light has a "continuous spectrum." On the other hand, excited atoms emit a "line spectrum" consisting of a set of monochromatic visible radiations.
Each element has a characteristic line spectrum that can be used to identify the element. Note that line emission spectra can also be obtained by heating a salt of a metal with a flame. For instance, common salt (sodium chloride) provides a strong yellow light to the flame coming from excited sodium, while copper salts emit a blue-green light and lithium salts a red light. The colors of fireworks are due to this phenomenon.
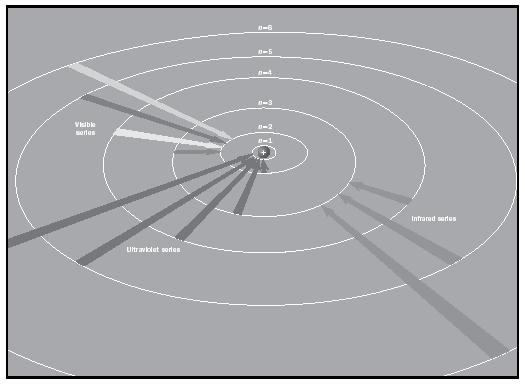
Scientists in the late nineteenth century tried to quantify the line spectra of the elements. In 1885 the Swedish school teacher Johann Balmer discovered a series of lines in the visible spectrum of hydrogen, the wavelengths of which could be related with a simple equation:
in which λ is wavelength, k is constant, a = 2, and b = 3, 4, 5, … This group of lines was called the Balmer series. For the red line b = 3, for the green line b = 4, and for the blue line b = 5. Similar series were further discovered: in the infrared region, the Paschen series (with a = 3 and b = 4, 5 … in the above equation), and much later in the ultraviolet region, the Lyman series (with a = 1 and b = 2, 3 …). In 1896 the Swedish spectroscopist Johannes Rydberg developed a general equation that allowed the calculation of the wavelength of the red, green, and blue lines in the atomic spectrum of hydrogen:
where n L is the number of the lower energy level to which an electron falls and n H is the number of the higher energy level from which it falls. R is called the Rydberg constant (1.0974 x 10 −7 m −1 ). R was later shown to be 2 π 2 me 4 Z 2 / h 3 c, where m is the mass of the electron, e is its charge, Z is the atomic number, h is Planck's constant, and c is the speed of light.
Bohr's Quantum Model
As noted earlier, Bohr had suggested the quantization of Ruthford's model of the atom. Although he was not aware of the work of Balmer and Paschen when he wrote the first version of his 1913 article, he had incorporated Planck's constant h into his model, which turned out to be an important decision. Bohr assumed that the absorption or emission of radiation can occur only by "jumps" of the electron from one stationary orbit to another. (See Figure 1.) The energy differences between two such allowed orbits then provided the characteristic frequencies of the emitted light.
Δ E = E n1 − E n2 = hν
Planck's constant h was named by Bohr the "quantum of action."
Bohr's theory was in close agreement with many experimental facts regarding one-electron atoms (the hydrogen atom and hydrogen-like atoms, such as He + and Li 2+ ), but it could not explain the "fine structure" of the spectral lines; that is, the fact that certain lines were actually a set of closely spaced lines. In 1915 and 1916 respectively, W. Wilson and A. Sommerfeld refined Bohr's theory by admitting elliptical orbits. However, it became evident to many physicists, including Bohr himself, that is was time for a scientific revolution.
Wave Character of Matter
To explain the photoelectric effect (the flow of electric current from a metal cathode when illuminated with visible or untraviolet light of suitable frequency), Albert Einstein attributed particulate (material) properties to light.
Thus, besides being an electromagetic wave, light could be accounted for in terms of particles called photons. This dual property of light led the French physicist Luis Victor de Broglie to propose, in 1925, that matter should have dual character too, exhibiting both particulate and wave properties. De Broglie's genius idea was soon after (in 1927) verified by experiment.
Schrödinger's Equation: Wave Mechanics
In 1926 the Austrian physicist Erwin Schrödinger published his famous equation. He started with de Broglie's concept of matter-waves and concluded that classical mechanics is not applicable to micromechanical problems. For a single particle moving in a field that gives it a potential energy V (e.g., a one-electron atom) the Schrödinger equation takes the following form:
where ψ is generally called the wave function, m is the particle's mass, h is Planck's constant, E is the particle's total energy, and V is its classical potential energy.
The Schrödinger Equation in Chemistry
The Schrödinger equation is the foundation of quantum mechanics. It is solved exactly for very few simple systems. In chemistry it is solvable without any approximation only for the hydrogen atom or hydrogen-like atoms (monoelectronic atomic cations). The mathematical solutions are called hydrogen orbitals, in general, an orbital is defined as a "one-electron wave function that obeys certain mathematical restrictions." Hydrogen orbitals depend on the values of the three quantum numbers— n (principal), l (angular momentum or "asimuthal"), and m l (magnetic).
The principal quantum number, n , identifies an electron's main shell, or energy level, and assumes integer values (1, 2, 3…). The azimuthal (or angular momentum) quantum number, l , describes the subshell, or sub-level, occupied by the electron and has values that depend on n , taking values from 0 to n −1. For s orbitals l = 0; for p orbitals l = 1; for d orbitals l = 2; and for the more complex f orbitals l = 3. Finally the magnetic quantum number, m l , identifies the particular orbital an electron is in and has values that depend on l , taking on values from 0 to + l or − l . For a given value of n , there can be only one s orbital, but there are three kinds of p orbitals, five kinds of d orbitals, and seven kinds of f orbitals.
Although it does not follow from the Schrödinger equation, there is a fourth quantum number, m s , that describes the spin of the electron. It can assume two values, +1/2 and −1/2. According to the Pauli Exclusion Principle no two electrons in an atom can have the same set of four quantum numbers. If two electrons have the same values for n (main shell), l (sub-shell), and m 1 (orbital), they must differ in spin. Each orbital in an atom can hold no more than two electrons, and they must be opposed in spin. Such a couple of electrons, opposite in spin, constitutes an electron pair.
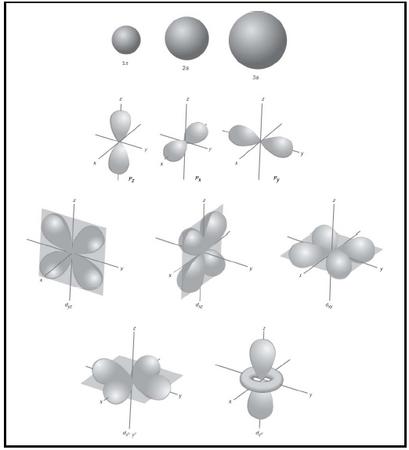
For practical reasons, various graphical representations of atomic orbitals are used. The most useful are boundary surfaces, such as those shown in Figure 2. These enclose regions of space where the electron described by the corresponding wave function (orbital) can be found with high probability (e.g., 99%); s orbitals are spherical, p orbitals are dumb-bell shaped, d orbitals have a four-leaf-clover shape, while f orbitals have complex shapes.
CLASSICAL AND QUANTUM PHYSICS
A fundamental difference between classical and quantum physics is that, while in classical physics the dynamic variables can be represented by ordinary algebraic variables, in quantum physics they are represented by "operators," which are expressed by mathematical matrices. This is a consequence of the fact that, while in classical physics any disturbance caused by the action of observation or measurement can, in principle, be calculated, in the submicroscopic world, the very action of observation or measurement of a dynamic variable disturbs the system. This is equivalent to the famous "uncertainty principle" of Heisenberg. The distinction between quantum (very small) and classical systems is generally made in units of h, Planck's constant. The size of h 6.6256 × 10 −34 J s) is extremely small for the macroscopic world, but for the sumicroscopic world of atoms, ions, molecules, etc., h is not small. Thus quantum mechanics is radically different from classical mechanics.
For many-electron atoms, no exact solutions to the corresponding Schrödinger equation exist because of the electron-electron repulsions. However, various approximations can be used to locate the electrons in these atoms. The common procedure for predicting where electrons are located in larger atoms is the Aufbau (building up) principle.
The Aufbau Principle
The arrangement of electrons in electron shells (K, L, M, N) is important for explaining both the chemical behavior of the elements and their placement in the periodic table. The first shell is called K ( n = 1), the second L ( n = 2), the third M ( n = 3), etc. Knowing the atomic number of an element, one places that number of electrons, one after another, into the various atomic orbitals, building up the atom until all the electrons have been added.
Three basic principles are followed:
- the principle of least energy (electrons seek the lowest available energy level),
- the Pauli exclusion principle (no more than two electrons per orbital), and
- Hund's rule (electrons of the same energy spread out before pairing up).
The principle of least energy would dictate that all electrons be located in the lowest energy K shell, in the 1 s orbital. However, the Pauli principle forbids this by requiring that no two electrons in an atom can be described by the same set of four quantum numbers. This leads to the restriction that an orbital cannot accommodate more than two electrons, and they must be of opposite spin. In this way, for a given value of n , the s orbital can accommodate no more than two electrons, the three p orbitals up to six electrons, the five d orbitals up to ten electrons, and the seven f orbitals up to fourteen electrons.
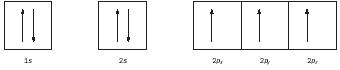
Hund's rule introduces one final restriction: electrons in degenerate (same energy) orbitals should spread out to fill as many orbitals as possible before pairing up. The seven electrons in the nitrogen atom would be placed in the 1 s , 2 s , and 2 p sublevels as shown below. (Electrons are shown as up-pointing arrows with spin = +½, or down pointing arrows with spin = −½).
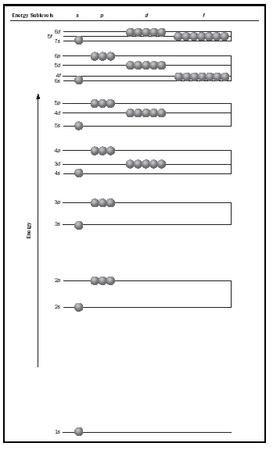
The lowest energy 1 s orbital fills first, then the 2 s orbital, then the last three electrons go into the three higher energy 2 p orbitals. In a hydrogen atom all orbitals within the same main shell have the same energy, but this is not true for atoms with many electrons because of the interactions among the electrons. Within a given main shell of a large atom, the s orbital is the lowest in energy, followed by the p orbitals, then the d orbitals, and finally the f orbitals. (See Figure 3.)
The electron configurations of atoms are more commonly shown as follows:
Nitrogen ( z = 7…) l s 2 2 s 2 2 p 3
This shows that the nitrogen atom has a nuclear charge of +7, and it therefore has seven electrons. Two electrons are in the first main shell in an s orbital, and the other five are in the second main shell, two in the s orbital and three in the p x , p y , and p z orbitals. Each can have as many kinds of orbitals (subshells) as the shell number. The first shell has one ( s ), the second has two ( s and p ), the third has three ( s , p , and d ), and the fourth has four ( s , p , d , and f ). The fifth would probably have five, if there were any atoms big enough to have a full fifth shell.
As atoms get larger, the order of filling electrons into orbitals gets more complicated. In the element Scandium (Sc), for example, the 4 s orbital is considered filled before the 3 d orbitals begin to fill. This may be explained in terms of the difference in shielding of the nucleus by the s and d electrons, as well as of interelectronic repulsion effects. It thus appears as if the 4 s orbital is lower in energy than the 3 d orbitals. (See Figure 3). The general order of filling of the various subshells is:
1 s <2 s <2 p <3 s <3 p <4 s <3 d <4 p <5 s <4 d <5 p <6 s http://4f5 d <6 p <7 s <5 f <6 d <7 p
The d electrons always come in one shell late, and the f electrons two shells late. This can be demonstrated with the lead (Pb) atom. Using the Aufbau procedure to show the order of filling, the electron configuration for the Pb atom is:
Lead (Pb, Z = 82): 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 2 3 d 10 4 p 6 5 s 2 4 d 10 5 p 6 6 s 2 4 f 14 5 d 10 6 p 2
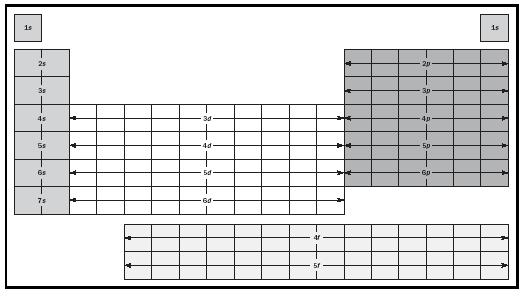
Perhaps the easiest way to determine the correct filling order is to use the periodic table. (See Figure 4). The square for each element represents the most recently added electron. In the first shell there are two s electrons; in the second there are two s and six p electrons; and in the third there are two s and six p electrons, and then ten more fill up the 3 d orbitals after the fourth shell has begun. The transition elements result from electrons filling in the d orbitals, and the lanthanide and actinide elements from electrons filling in the f orbitals.
Electron configurations for the various elements in group 5A of the periodic table (but not indicating the order of the filling) are shown below:
Nitrogen (N, Z = 7): ls 2 2s 2 2p 3
Phosphorus (P, Z = 15): 1s 2 2s 2 2p 6 3s 2 3p 3
Arsenic (As, Z = 33): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 3
Antimony (Sb, Z = 51): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 5s 2 5p 3
Bismuth (Bi, Z = 83): ls 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 4f 14 5s 2 5p 6 5d 10 6s 2 6p 3
Note that the electron configurations for the larger atoms can get rather cumbersome, but they can be readily shortened by using the noble gas core convention.
Nitrogen [He] 2s 2 2p 3
Phosphorus [Ne] 3s 2 3p 3
Arsenic [Ar] 3d 10 4s 2 4p 3
Antimony [Kr] 4d 10 5s 2 5p 3
Bismuth [Xe] 4f 14 5d 10 6s 2 6p 3
The noble gas core represents all electrons contained in an atom of noble gas. The similar chemical properties of the elements in the 5A group is attibuted to the similar arrangement of the outer shell electrons of all the members of the group: ns 2 np 3 . The outermost shell is vital for determining the chemical properties of the elements and is called the valence shell . Similar regularities appear in the other groups of the periodic table.
A number of elements show deviations from the predicted configurations. For instance, instead of the predicted configuration KL…( n −1) d 4 ns 2 , we have KL…( n −1) d 5 ns 1 for the chromium (Cr) and molybdenum (Mb). In such cases, we speak of the preferred stability of the half-filled ( d 5 ) or filled ( d 10 ) d subshell. It might also be noted that with atoms of the heavy elements relativistic effects play a role, because of the higher velocities (approaching the speed of light) of the inner shell electrons, caused by the high Z values and the accompanying contraction of the inner shells.
SEE ALSO Atomic Nucleus ; Bohr, Niels .
Georgios Tsaparlis
Bibliography
Atkins, Peter, and Jones, Loretta (2002). Chemical Principles: The Quest for Insight , second edition. New York: W. H. Freeman.
Chang, Raymond (2002). Chemistry , seventh edition. Boston: McGraw-Hill.
Fong, P. (1962). Elementary Quantum Mechanics. Reading, MA: Addison-Wesley.
Fricke, M. (1976). "Quantum Mechanics." In Method and Appraisal in the Physical Sciences: The Critical Background to Modern Science, 1800–1905 , ed. C. Howson. New York: Cambridge University Press.