Kinetics

Chemical kinetics is the study of the rates of chemical reactions. Such reaction rates range from the almost instantaneous, as in an explosion, to the almost unnoticeably slow, as in corrosion. The aim of chemical kinetics is to make predictions about the composition of reaction mixtures as a function of time, to understand the processes that occur during a reaction, and to identify what controls its rate.
Rates and Rate Laws
The rate of a chemical reaction is defined as the rate of change of the concentration of one of its components, either a reactant or a product. The experimental investigation of reaction rates therefore depends on being able to monitor the change of concentration with time. Classical procedures for reactions that take place in hours or minutes make use of a variety of techniques for determining concentration, such as spectroscopy and electro-chemistry. Very fast reactions are studied spectroscopically. Spectroscopic procedures are available for monitoring reactions that are initiated by a rapid pulse of electromagnetic radiation and are over in a few femtoseconds (1 fs = 10 −15 s).
The analysis of kinetic data commonly proceeds by establishing a rate law, a mathematical expression for the rate in terms of the concentrations of the reactants (and sometimes products) at each stage of the reaction. For instance, it may be found that the rate of consumption of a reactant is proportional to the concentration of the reactant, in which case the rate law is
Rate = k [Reactant]
where [Reactant] denotes the concentration of the reactant and k is called the rate constant. The rate constant is independent of the concentrations of any species in the reaction mixture but depends on the temperature. A reaction with a rate law of this form is classified as a first-order rate law. More generally, a reaction with a rate law of the form
Rate = k [Reactant A] a [Reactant B] b …
is said to be of order a in A, of order b in B, and to have an overall order of a + b + …. Some rate laws are far more complex than these two simple examples and many involve the concentrations of the products.
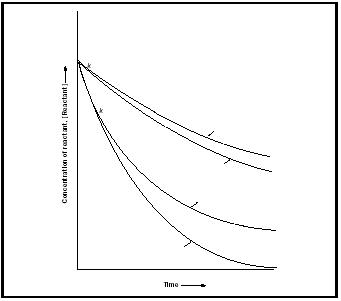
The advantage of identifying the reaction order is that all reactions with the same rate law (but different characteristic rate constants) behave similarly. For example, the concentration of a reactant in a first-order reaction decays exponentially with time at a rate determined by the rate constant
[Reactant] = [Reactant] 0 e −kt
where [Reactant] 0 is the initial concentration of the reactant. On the other hand, all second-order reactions lead to the following time-dependence of the concentration:
Figure 1 shows the time-dependence predicted by these expressions. It is common to report the time-dependence of first-order reactions in terms of the half-life, t ½ , of the reactant, the time needed for its concentration to fall to half its initial value. For a first-order reaction (but not for other orders)
Thus, reactions with large rate constants have short half-lives.
Reaction Mechanisms
The identification of a rate law provides valuable insight into the reaction mechanism, the sequence of elementary steps by which a reaction takes place. The aim is to identify the reaction mechanism by constructing the rate law that it implies. This procedure may be simplified by identifying the rate-determining step of a reaction, the slowest step in a sequence that determines the overall rate. Thus, if the proposed mechanism is A → B followed by B → C, and the former is much faster than the latter, then the overall rate of the reaction will be equal to the rate of A → B, for once B is formed, it immediately converts into C.
In general, for a mechanism of many steps (including their reverse), the construction of the overall rate law is quite difficult, requiring an approximation or a computer for a numerical analysis. One common approximation
is the steady-state assumption, in which the net rate of formation of any intermediate (B in the present example) is set equal to zero. A hazard of using kinetic information to identify a reaction mechanism, however, is that more than one mechanism might result in the same rate law, especially when approximate solutions are derived. For this reason, proposed reaction mechanism must be supported by additional evidence.

The Origin of Reaction Rates
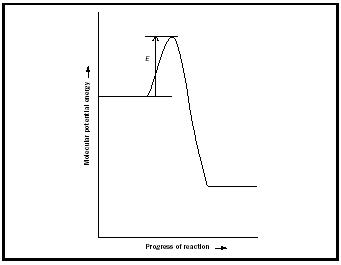
Once a reaction mechanism has been identified, attention turns to the molecular properties that govern the values of the rate constants that occur in the individual elementary steps. A clue to the factors involved is provided by the experimental observation that the rate constants of many reactions depend on temperature according to the Arrhenius expression
where E a is called the activation energy.
The simplest model that accounts for the Arrhenius expression is the collision theory of gas- phase reaction rates, in which it is supposed that reaction occurs when two reactant molecules collide with at least a minimum kinetic energy (which is identified with the activation energy, Figure 2). A more sophisticated theory is the activated complex theory (also known as the transition state theory ), in which it is supposed that the reactants encounter each other, form a loosened cluster of atoms, then decompose into products.
Reactions in solution require more detailed consideration than reactions in gases. It is necessary to distinguish between "diffusion-controlled" and
"activation-controlled" reactions. In a diffusion-controlled reaction, the rate is controlled by the ability of the reactants to migrate through the solvent and encounter each other. In an activation-controlled reaction, the rate is controlled by the ability of the reactants that have met each other to acquire enough energy to react.
The rate of a reaction may also be increased by finding a catalyst , a substance that takes part in a reaction by providing an alternative pathway with a lower activation energy but is regenerated in the process and is therefore not consumed. Catalysis is the foundation of the chemical industry and a great effort is made to discover or fabricate efficient, economical catalysts. It is also the foundation of life, because the biological catalysts known as enzymes (elaborate protein molecules) control almost every aspect of an organism's function.
SEE ALSO Catalysis and Catalysts ; Enzymes ; Physical Chemistry .
Peter Atkins
Bibliography
Atkins, Peter, and de Paula, Julio (2002). Physical Chemistry. New York: W.H. Freeman.
Atkins, Peter, and Jones, Loretta (2001). Chemical Principles. New York: W.H. Freeman.
Laidler, K. J. (1987). Chemical Kinetics. New York: Harper and Row.
Pilling, M. J., and Seakins, P. W. (1996). Reaction Kinetics. London: Oxford University Press.
Comment about this article, ask questions, or add new information about this topic: