Stoichiometry

Stoichiometry refers to the ratios of products and reactants in a chemical reaction. It is a fundamental concept in chemistry, and we shall give a more exact description later.
Early Stoichiometry
The masses of the starting materials and of the products of chemical reactions were of obvious interest to early chemists. The earliest measurements may have been made by prehistoric metal workers who weighed a metal ore with a primitive balance and compared the weight with that of the extracted metal. Weighing was the most common and most accurate measurement that chemists could make for many centuries. An early example is the work of Belgian chemist Johann van Helmont in the early seventeenth century. Van Helmont weighed a large pot containing a growing plant at intervals and tried to show that the gain in weight was fully accounted for by the water added. He did not measure the carbon dioxide gas taken up or the oxygen released by the plant and so his conclusion was not valid, although the measurements were roughly correct.
Whether or not pure substances have the same proportion by mass of their constituents was by no means initially obvious. Around 1800 two French chemists, Claude Berthollet and Joseph Proust, supported opposite views on this topic. If a metal such as lead is heated in air, there is a gradual color change as lead oxide is slowly formed. Berthollet argued for a combination of "indefinite proportions" as this transformation occurs: the reactant is lead, the product is lead oxide, and there is an indefinite number of intermediates . Proust argued for "definite proportions" in that the system would at all times consist only of lead mixed with lead oxide (for simplicity we can ignore that more than one oxide of lead exists). The ratio of lead to lead oxide would change as the reaction proceeded but the system would have only two components. The wide acceptance of English
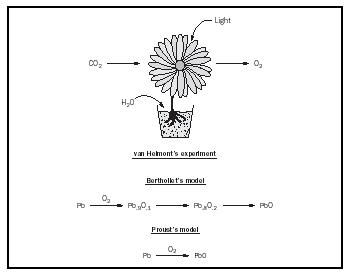
chemist and physicist John Dalton's atomic theory a few years later convinced most chemists that Proust was right and that there was a Law of Definite Proportions for pure compounds.
The term "stoichiometry" was devised by German chemist Jeremias Richter in 1792 to describe the measurement of the combining ratios of chemical elements by mass. The term has since been expanded to include the combining ratios of substances in any chemical reaction. Richter studied mathematics with philosopher Immanuel Kant and wrote a thesis on the use of mathematics in chemistry. He was convinced that all chemical changes could be described in terms of simple whole-number ratios. He put forward the Law of Reciprocal Proportions, stating that if two chemical elements unite separately with a third element, the proportion in which they unite with the third element will be the same or a multiple of the proportion in which they unite with each other. This law has disappeared from most chemistry textbooks, but a companion law, the Law of Multiple Proportions, has survived.
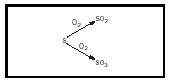
The Law of Multiple Proportions states that when two elements combine to form two or more different compounds, the weights of one compound that can combine with a given weight of the second compound form small whole number ratios. For example, consider one experiment in which 10.0 grams of sulfur is combined with 10.0 grams of oxygen to form an oxide of sulfur, and another experiment under different conditions in which 3.21 grams of sulfur is combined with 4.82 grams of oxygen to form a different oxide. For each 10.0 grams of sulfur used in the second experiment, 15.0 grams (4.82 × 10.0/3.21) of oxygen is used. The ratios of the masses of oxygen that combine with a fixed mass of sulfur are 10.0:15.0, which is equal to the whole number ratio 2:3. This conforms to the Law of Multiple Proportions. (See Figure 2.)
The Laws of Reciprocal and Multiple Proportions have ceased to have predictive scientific value. Their importance lies in the fact that they provided evidence that Dalton needed in 1807 to postulate his atomic theory. The reason for Richter's whole number ratios has since become obvious: the simple ratios occur because atoms, although having different masses, react in simple ratios. Dalton's insistence that atoms cannot be split in chemical reactions holds true in modern chemistry.
Balancing Chemical Equations
Chemical equations are an indispensable way of representing reactions. They are routinely used to calculate masses of reactants and products. In the case of the examples used above for the Law of Multiple Proportions, the equations are:
S + O 2 = SO 2 (1)
2S + 3O 2 = 2SO 3 (2)
Note that we do not write the second equation as:
S + 3O = SO 3 (3)
because O (an oxygen atom) means something very different from O 2 (an oxygen molecule). Chemical equations also introduce the concept of a limiting reagent , or the reactant that is used up first in a reaction, when one or more components are in excess of the stoichiometric amount.
The balancing of chemical equations is a common exercise in elementary stoichiometry. It is not always appreciated, however, that some chemical equations are ambiguous in that they can be balanced in more than one way. Consider, for example, the following equation:
H + + ClO 3 − + Cl − → Cl 2 + ClO 2 + H 2 O (4)
where the dashed arrow signifies an unbalanced equation. It may be balanced as follows:
4H + + 2ClO 3 − + 2Cl − = Cl 2 + 2ClO 2 + 2H 2 O (5)
Both sides of this equation have four H-atoms, six O-atoms, four Clatoms, and a total charge of zero. Equation 5 can also be balanced as:
16H + + 4ClO 3 − + 12Cl − = 7Cl 2 + 2ClO 2 + 8H 2 O (6)
Here both sides have 16 H-atoms, 12 O-atoms, 16 Cl-atoms, and a total charge of zero. How can both equations balance, and which is correct? To answer the first question, many equations can be written as the sum of two or more component reactions. In this case the following related reaction can be used:
8H + + 2ClO 2 + 8Cl − = 5Cl 2 + 4H 2 O (7)
If equation (5) is doubled and added to equation (7), the result is equation (6). Alternatively, equation (5) could be tripled and added to equation(7) to obtain yet another balanced equation with the same reactants and products in different stoichiometric amounts. There is therefore no limit to the number of balanced equations.
Deciding which equation is "correct" is often difficult because one of many competing pathways may take precedence in a reaction, depending on the energy requirements of the system (the thermodynamic limitations) and the speed of the reactions (the kinetics of the system). In the example above, analysis shows that equation (5) is thermodynamically unfavorable at room temperature while equation (6) is favorable.
Non-Stoichiometric Compounds
Most of chemistry is governed by simple whole-number ratios of molecules and atoms. Simple stoichiometry, although valid for the vast majority of mole ratios, is not universal: there are compounds with non-integral mole ratios. Substances such as alloys and glasses created problems for the initial acceptance of Dalton's atomic theory. There are, in addition, simple nonstoichiometric compounds that have varying ratios of constituent atoms. Such compounds are generally crystalline solids with defects in their crystal lattices; the lack of simple stoichiometry may give them important properties. Wustite, an oxide of iron, is an example of a non-stoichiometric compound. Its formula can be written Fe n O 1.000, where n may have values varying from 0.88 to 1.00 and its physical and chemical properties will vary somewhat depending on the value of n.
Current Applications of Stoichiometry
Most chemical reactions are complex, occurring via many steps. In such cases, can an overall reaction be written that describes the stoichiometry of a system under consideration? Consider an example in which sulfur is burned in oxygen to simultaneously form sulfur dioxide (mostly) and some sulfur trioxide:
S + O 2 → SO 2 (8)
S + 1.5 O 2 → SO 3 (9)
(Note that the "1.5" in reaction (9) means 1.5 moles, not 1.5 molecules.) If the two reactions are added, the resulting equation is: 2S + 2.5 O 2 → SO 2 + SO 3 . This representation of the reaction is plainly wrong because it states that one mole of SO 2 is obtained for every mole of SO 3 , whereas most of the products consist of SO 2. The reason for this inconsistency is that the arrows in reactions (8) and (9) mean "becomes"; they are not equivalent to equals signs because they involve time dependence. In order to obtain an overall stoichiometric description of the reaction, both equations (8) and (9) are necessary, as is knowledge about their relative importance in the over-all reaction.
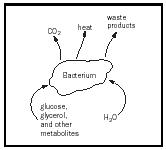
Stoichiometry also has biochemical applications. In this case, the systems are biological networks. A typical biological network might be the central metabolism of a bacterium living in the gut under anaerobic conditions. This system consists of multiple processes that occur simultaneously involving reactions catalyzed by many enzymes. At the same time that reactants such as glucose are being consumed, many different metabolic products are being formed, and the combined reactions provide energy for the overall process. By doing experiments in which some genes in the bacterium have been deactivated, and then analyzing the "metabolic balance sheets," it becomes possible to identify which genes are essential for the overall process and which have no effect. It then becomes possible to predict the properties of mutants of the bacterium.
SEE ALSO Equations, Chemical .
Sidney Toby
Bibliography
Chang, R. (1994). Chemistry, 5th edition. New York: McGraw-Hill.
Cornish-Bowden, Athel, and Cardenas, Maria Luz (2002). "Metabolic Balance Sheets." Nature 420: 129–130.
Hill, J. W., and Petrucci, R. H. (2002). General Chemistry, 3rd edition. Upper Saddle River, NJ: Prentice Hall.
Jones, L., and Atkins, P. (2000). Chemistry, 4th edition. New York: W. H. Freeman.
Toby, Sidney, and Tobias, Irwin (2003). "What Is the Overall Stoichiometry of a Complex Reaction?" Journal of Chemical Education 80: 520–523.
Zumdahl, S. S. (1997). Chemistry, 4th edition. Boston: Houghton Mifflin.
Comment about this article, ask questions, or add new information about this topic: