Reaction Rates

In chemistry, there is much interest in how quickly reactant molecules are transformed into product molecules and in the reaction steps or "mechanism" by which the chemical transformation occurs. We focus here on the speed with which chemical transformations occur, hence the title "reaction rates."
To calculate the impact of changing reactant concentrations, temperature, or pressure on a chemical reaction rate, a reliable quantitative measure of the change in the concentration of a reactant or product chemical species versus the change in time is needed. The first quantitative reaction rate study, carried out by Ludwig Wilhelmy in 1850, illustrates this. He followed the course of the "inversion of sucrose" in aqueous solution
by observing a gradual rotation of the plane of polarized light passed through the solution over time. Sucrose rotates the plane of polarized light clockwise, whereas fructose rotates the plane of polarized light more strongly counterclockwise. Wilhelmy thus found that the concentration c of sucrose decreases with time t according to the following equation
− dc / dt = k 1 c
where k 1 is the rate constant, a factor that has a temperature and pressure dependence but does not have a concentration dependence. This is called a first-order rate expression and k 1 is called a first-order rate constant, because the concentration c is raised to the first power in this rate equation. The half-line of this reaction, the time required for half of the sucrose
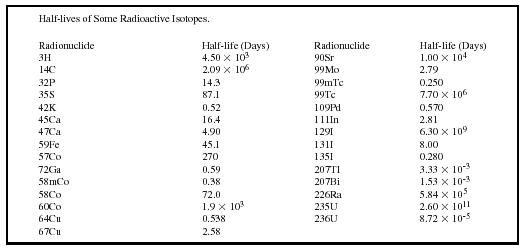
| Half-lives of Some Radioactive Isotopes. | |||
| Radionuclide | Half-life (Days) | Radionuclide | Half-life (Days) |
| 3H | 4.50 × 10 3 | 90Sr | 1.00 × 10 4 |
| 14C | 2.09 × 10 6 | 99Mo | 2.79 |
| 32P | 14.3 | 99mTc | 0.250 |
| 35S | 87.1 | 99Tc | 7.70 × 10 6 |
| 42K | 0.52 | 109Pd | 0.570 |
| 45Ca | 16.4 | 111In | 2.81 |
| 47Ca | 4.90 | 129I | 6.30 × 10 9 |
| 59Fe | 45.1 | 131I | 8.00 |
| 57Co | 270 | 135I | 0.280 |
| 72Ga | 0.59 | 207T1 | 3.33 × 10 −3 |
| 58mCo | 0.38 | 207Bi | 1.53 × 10 −3 |
| 58Co | 72.0 | 226Ra | 5.84 × 10 5 |
| 60Co | 1.9 × 10 3 | 235U | 2.60 × 10 11 |
| 64Cu | 0.538 | 236U | 8.72 × 10 −5 |
| 67Cu | 2.58 | ||
initially present in solution to react, is given for a first-order reaction by the expression
t 1/2 = ln 2/ k 1
where the first-order rate constant k 1 has the units of reciprocal time. This is a general expression for all first-order reactions.
Overall Reaction Order
When the sucrose inversion reaction was later run in nonaqueous solvents it was recognized that a better description of the rate of disappearance of sucrose S is given by the following equations:
S + H + ⇌ SH +
Kc = [ SH + ]/[ S ][ H + ]
− d[S] / dt = k[SH + ][H 2 O] = kK c [S][H + ][H 2 O]
Thus, the reaction rate is first-order in sucrose, first-order in the catalyst H + , and first-order in H 2 O. The reaction is said to be "third-order overall," third because of the sum of the powers on the three concentration factors.
The "initial rate method" is usually used to deduce reaction order from experimental rate data. This means that the reaction rate is determined over a short range of times after mixing reactants to avoid the complicating effects of reaction products undergoing further reactions. The initial reaction rate R = k [ A ] a [ B ] b [ C ] c … is measured several times, with the concentrations of the reactants A, B, C, and so on systematically varied. Then, taking the logarithm of both sides of each rate equation log R = log k + a log[ A ] + b log[ B ] + c log[ C ] … the several resulting simultaneous linear equations for the values of a, b, c, and so on can be solved. Often, all but one of the reactant concentrations are kept constant, and the concentration dependence of the variable reactant is then most easily determined.
Temperature Dependence of Rates
In 1889 Svante Arrhenius noted that an increase in Kelvin temperature T caused the rate constant k of many reactions to increase according to the relation
k = Ae −Ea/RT
or
ln / k = ln A − Ea / RT
where the activation energy E a is related to the minimum amount of energy that a reactant molecule must acquire from collisions or some other form of excitation to go on to form reaction products. R is the perfect gas (ideal gas) constant.
If the rate constant k for a reaction is determined at several different temperatures, all that one needs to do to obtain a numerical value of E a is to construct a plot of ln k on the vertical axis versus 1/ T on the horizontal axis. If the chemical reaction obeys the Arrhenius equation, a straight line plot of the experimental data having a negative slope is obtained. The slope of this line is equal to − E a /R . Readers living in temperate climates will recall that the rate at which crickets chirp gradually declines in autumn as out-side temperatures become cooler. If the natural logarithm of the frequency of the chirping of crickets is plotted versus the reciprocal of the Kelvin temperature, the observer deduces from the slope of the resulting straight line that the activation energy for chirping is about E a = 5 × 10 4 joules/mole.
If k 1 is the rate constant for a given reaction at a Kelvin temperature T 1 , we may estimate the magnitude k 2 of the rate constant of that reaction at some other temperature T 2 from the following alternative form of the Arrhenius equation:
A familiar rule in chemistry states that "the rate of a chemical reaction doubles for each increase in temperature of ten degrees." From this second form of the Arrhenius equation it becomes clear that the moderate success of this rule of thumb proceeds from the fact that for many chemical reactions the activation energy E a has a magnitude in the general ballpark area of 5 × 10 4 joules/mole.
The Activated Complex
A chemical reaction in which a diatomic molecule A–B collides end-on with an atom C, to form a diatomic molecule B–C and an atom A, can be depicted as occurring on a surface within a theoretical three-dimensional space in which the vertical axis is potential energy and the other two axes are the A–B and the B–C bond distances. In 1931 Henry Eyring and Michael Polanyi took reaction rate studies to the individual molecule level by calculating a potential energy surface for the colinear gas phase reaction
D + H 2 → DH + H
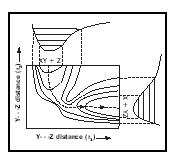
where D denotes the deuterium isotope of hydrogen. They visualized the passage of the system from reactants to products as occurring via a linear configuration of the three atoms corresponding to the top of a potential energy barrier that they called the "activated complex." This entity had a presumed lifetime of only 10 −13 seconds or less, and no one in the 1930s foresaw that activated complexes would finally be observed experimentally (in 1987) by Ahmed Zewail using femtosecond duration (10 −15 seconds) laser pulses.
In 1935 Eyring and Polanyi independently formulated a "transition state theory" expression for the A-term in the Arrhenius equation pertaining to the rate constant of a gas phase reaction. Their work was based on the idea that a chemical equilibrium exists between the reactant species and the activated complex, even though some of the activated complex species must be "leaking" over the top of the potential energy barrier and forming products. Powerful concepts that still have wide application in explaining reaction rates emerged from transition state theory. For instance, gas phase reactions between two large molecules are typically slower than one would predict using a billiard ball collision model of reaction rates. This is because much of the collision energy can be stored unreactively in the internal vibrations of a collisionally excited molecule.
Pressure Dependence of Rates
Another application of transition state theory is its explanation of the effect of pressure on reaction rates. Increasing pressure by a factor of 10 3 decreases the rate constant for a ring-closure reaction
by a factor of 1.3 (where L is the bidentate ligand 1,10-phenanthroline and the solvent is liquid toluene at 25°C). The change in volume in going from reactants to activated complex is Δ V ≠ = +6.1 cm 3 mol −1 . Applying le Chatelier's principle to the quasi-equilibrium between reactants and activated complex molecules, the transition state theory point of view maintains that the increase in pressure favors formation of reactants over formation of activated complexes, because the reactants are more compact. With fewer activated complexes present, the reaction-yielding product from activated complexes slows down.
Reaction Time Scales
Many important reactions, such as the conversion of atmospheric nitrogen and hydrogen into ammonia, are very slow and remain that way until a catalyst (in this case iron oxide) is identified. In our bodies, enzymes can function as catalysts to speed up essential reactions. In order to understand reaction mechanisms, chemists focus on discrete reaction steps and often need very short-term experimental methods to follow rates of individual reaction steps. For instance, Manfred Eigen and Leo De Maeyer (1955) used an electrical conductance "relaxation method" to measure the rate of the reaction
in liquid water. They found a rate constant k = 1.4 × 10 11 liters mol −1 s −1 at 25°C (77°F) by measuring relaxation times (roughly reaction half-lives) on a time scale of tens of microseconds. In recent years femtosecond laser pulses have proved to be the most powerful experimental tool for elucidating the details of chemical reaction steps and their rates. Zewail has speculated that attosecond (10 −18 second) laser pulses will be achieved that will enable scientists to track the paths of electrons within molecules as the molecules undergo chemical reactions.
SEE ALSO Catalysis and Catalysts .
Edward M. Eyring
Bibliography
Brown, Theodore L.; LeMay, H. Eugene, Jr.; and Bursten, Bruce E. (2000). "Chemical Kinetics." In Chemistry: The Central Science, 8th edition. Upper Saddle River, NJ: Prentice Hall.
Zewail, Ahmed H. (2000). "Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond Using Ultrafast Lasers (Nobel Lecture)." Angewandte Chemie. International Edition 39: 2587–2631.
Comment about this article, ask questions, or add new information about this topic: