Molecular Modeling
A model is a semblance or a representation of reality. Early chemical models were often mechanical, allowing scientists to visualize structural features of molecules and to deduce the stereochemical outcomes of reactions. The disadvantage of these simple models is that they only partly represent (model) most molecules. More sophisticated physics-based models are needed; these other models are almost exclusively computer models.
Two major categories of physics-based, computational molecular models exist: macroscopic and microscopic. Macroscopic models describe the coarse-grained features of a system or a process but do not describe the atomic or molecular features. Microscopic or atomistic models take full account of all atoms in the system.
Atomistic modeling can be done in two ways: by applying theory or by using fitting procedures. The fitting procedures are attempts to rationalize connections between molecular structure and physicochemical properties (quantitative structure property relationships, QSPR), or between molecular structure and biological response (quantitative structure activity relationships, QSAR). Usually, a molecule's biological response is regressed onto a set of molecular descriptors.
Here C is the minimum concentration of a compound that elicits a response to an assay of some sort (e.g., an LD 50 , or something else), b 0 is a constant, b i is the least-squares multiple regression coefficient, and D i is the molecular descriptor. For example, the best model for determining the retention index (RI) of drug molecules on a gas-liquid chromatography column was found to be RI = 9.92 MW − 3.11 (number of ring atoms) + 139 (number of ring nitrogens) + 296 (total σ charge) + 921 Σ atomic IDs on nitrogen − 335 6 XCH − 211 3 XC − 49 2 κ α − 1958 (X and κ are topological and topographical descriptors). One can then predict an unknown drug's RI very accurately by substituting the values of the descriptors for that drug into the above equation. There are no rules about what kind of descriptors may or may not be used, but descriptors often include information about molecular size, shape, electronic effects, and lipophilicity. Microscopic modeling based on fitting methodologies requires the use of existing data to create a model. The model is then used to predict the properties or activities of as yet unknown molecules.
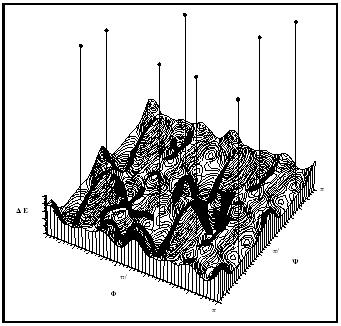
The other approach to microscopic molecular modeling implements theory, and uses various sampling strategies to explore a molecule's potential energy surface (PES). Knowing a molecule's PES is convenient, because one can interpret directly from it the molecule's shape and reactivity. Popular modeling tools used for determining PES are shown in Figure 1.
Quantum Mechanics (QM). The objective of QM is to describe the spatial positions of electrons and nuclei. The most commonly implemented QM method is the molecular orbital (MO) theory, in which electrons are allowed to flow around fixed nuclei (the Born-Oppenheimer approximation) until the electrons reach a self-consistent field (SCF). The nuclei are then moved, iteratively, until the energy of the system can go no lower. This energy minimization process is called geometry optimization.
Molecular Mechanics (MM). Molecular mechanics is a non-QM way of computing molecular structures, energies, and some other properties of molecules. MM relies on an empirical force field (EFF), which is a numerical recipe for reproducing a molecule's PES. Because MM treats electrons in an implicit way, it is a much faster method than QM, which treats electrons explicitly. A limitation of MM is that bond-making and bond-breaking processes cannot be modeled (as they can with QM).
Molecular Dynamics (MD). Energy-minimized structures are motionless and, accordingly, incomplete models of reality. In molecular dynamics, atomic motion is described with Newtonian laws: F i (t)=m i a i , where the force F i exerted on each atom a i is obtained from an EFF. Dynamical properties of molecules can be thus modeled. Because simulation periods are typically in the nanosecond range, only inordinately fast processes can be explored.
Monte Carlo (MC). The same EFFs used in the MM and MD methods are used in the Monte Carlo method. Beginning with a collection of particles, the system's initial energy configuration is computed. One or more particles are randomly moved to generate a second configuration, whose energy is "accepted" for further consideration, or "rejected," based on energy criteria. Millions of structures on the PES are sampled randomly. Averaged energies and averaged properties are thus obtained.
Most atomistic modeling involves the exploration of a complex and otherwise unknown PES. Simple energy minimization with QM or MM locates a single, stable structure (the local minimum) on the PES, which may or may not be the most stable structure possible (the global minimum). MD and MC sampling methods involve a more complete searching of the PES for low energy states and, accordingly, are more time-consuming.
Bibliography
Leach, A. R. (2001). Molecular Modeling: Principles and Applications, 2nd edition. Englewood Cliffs, NJ: Prentice-Hall.
Lipkowitz, Kenneth B., and Boyd, D. B., eds. (1990–2002). Reviews in Computational Chemistry, Vols. 1–21. New York: Wiley-VCH.
Von Rague Schleyer, P., ed. (1998). Encyclopedia of Computational Chemistry, Vols. 1–5. Chichester, U.K.: John Wiley.
Comment about this article, ask questions, or add new information about this topic: