Gases

A gas is a state of matter in which a substance does not have a specific shape or volume of its own, but adopts the form and size of its container. It was the early-seventeenth-century Flemish chemist-physician Jan Baptista van Helmont who coined the word "gas" (from the Greek chaos ) in order to convey the idea that a gas had an indefinite shape and size. This is an apt name because, as was later hypothesized and confirmed, gas molecules are distributed uniformly throughout a container without any apparent spatial organization, and they undergo incessant, seemingly chaotic, random motion.
A liquid, like a gas, has no shape of its own, but it does have a definite volume. Both states of matter are referred to as fluids because of their mobility, or tendency to flow. A gas is actually a low density fluid because the molecules are much farther apart than in a liquid where molecules are in close contact with each other. For example, at room temperature and at atmospheric pressure the density of air is about 0.0012 grams (0.000042 ounces) per cubic centimeter (g/cm 3 ), whereas the density of liquid air is approximately 0.810 g/cm 3 (at its normal boiling point of −209°C, or −344°F). This corresponds to an average separation between molecules in the gas phase that is about nine times larger than that for the liquid. A liquid is thus called a condensed phase—or a high density fluid—and is roughly 1,000 times more dense than a gas.
A compound exists in the gaseous state because the attractive forces between the molecules are weak and/or the average distance between them is large. Liquifaction, or condensation of the gas, may occur if the kinetic energy of the molecules is reduced (by cooling) and/or the intermolecular distance is made smaller (by compression).
Gas Properties
There are four intrinsic, measurable properties of a gas (or, for that matter, any substance): its pressure P , temperature T , volume (in the case of a gas, the container volume) V , and mass m , or mole number n. The gas density d is a derived quantity, which is m/V. Before the relationships between these properties for a gas are discussed, the units in which they are usually reported will be outlined.
Pressure is defined as force per unit area. In the International System of Units (SI, or mks), unit pressure corresponds to one newton per square meter, which is denoted as one pascal or Pa (named after Blaise Pascal, the seventeenth-century French scientist). There are several other, more commonly used pressure units, however. One is the atmosphere or atm; it is based on the magnitude of the pressure actually exerted by Earth's atmosphere at sea level. Because atmospheric pressure varies, one atmosphere is simply defined as the pressure that is exerted by a 760-mm-high column of mercury, a dense liquid sometimes used to measure pressures. Note that 760 mm is equivalent to 29.91 inches, which is close to the value sometimes cited in weather reports of atmospheric pressure. Another pressure unit is the torr (named after the seventeenth-century Italian scientist Evangelista Torricelli). One torr is equivalent to one mm Hg.
One pascal corresponds to a very small pressure as compared with one atm, that is, 1 Pa = 9.86923 × 10 −6 atm. The bar is another commonly used pressure unit. One bar is defined as 10 5 Pa and is equal to 750 torr.
Temperature is often reported in degrees Celsius. One Celsius degree is defined as 1/100 of the temperature difference between boiling water and freezing water (both at 1 atm pressure). In this scale, the temperature of pure water at its freezing point is 0°C (32°F) at 1 atm pressure. Another important temperature scale is the absolute temperature. The absolute temperature of pure liquid water in coexistence with ice and water vapor (the triple point) is defined as exactly 273.16 kelvins (K). This condition corresponds to 0.01°C, and thus the relationship between the Celsius (t) and Kelvin scales (T) is
t = T − 273.15°
The significance of the Kelvin scale is that 0 K represents the lowest temperature that can, in theory, be attained and corresponds to the condition in which molecular translational and rotational motion ceases.
The SI unit of volume is the cubic meter (m 3 ), but in most scientific applications, volumes are usually measured in cubic centimeters (cm 3 ) or liters (L). One liter contains 1,000 milliliters (mL), or equivalently, 1,000 cm 3 .
The SI unit of quantity is called the mole (symbol n and abbreviation mol). It is derived from the Latin moles (meaning "a mass"). One mole of a substance contains Avogadro's number of elementary units of the substance. Because atoms and molecules are extremely small entities, Avogadro's number (N A ) is incomprehensibly large, 6.022 × 10 23 particles/mol. Thus, one mole of hydrogen atoms contains 6.022 × 10 23 H atoms, one mole of sucrose molecules consists of 6.022 × 10 23 sucrose molecules, and so forth.
Relationships among Gas Properties
From the earliest days of quantitative inquiry, scientists have sought to uncover the mathematical relationships that describe natural phenomena, including the properties of gases. Because there are four fundamental properties of a gas, namely, P, T, V, and n, discovering the relationship between any two requires that the other two properties be kept constant. Some of the earliest quantitative studies of gases were reported in the mid-1600s by British chemist Robert Boyle, who found that for a fixed amount of a gas at a specific temperature (i.e., constant n and T ), the volume was inversely proportional to the applied pressure. This V-P relationship, known as Boyle's law, is represented as
V = c/P
or
PV = c
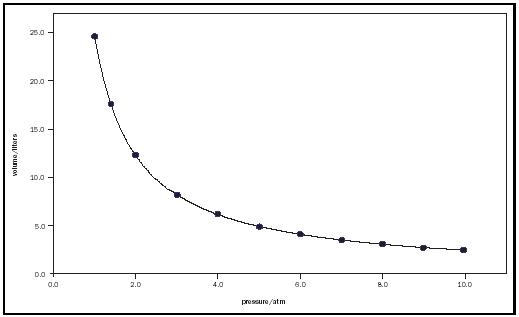
where c is an experimental constant that depends on the amount of gas and its temperature.
Figure 1 illustrates Boyle's law with a plot of the volume occupied by one mole of a gas at 300 K as a function of pressure.
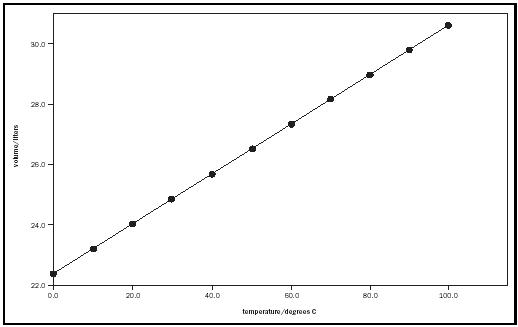
In the later part of the eighteenth century, French chemist Jacques Charles studied the relationship between the volume of a fixed amount of gas and its temperature, while keeping the gas at constant pressure. He found that V was a linear function of the temperature. Figure 2 graphically represents this relationship, known as Charles's law, with a plot of the gas volume versus the temperature in Celsius, t.
Mathematically, Charles's law is expressed as
V = a + bt
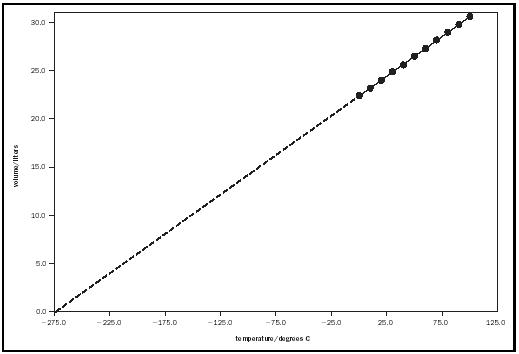
where a and b are constants. The same data are plotted with expanded scales in Figure 3 to illustrate the fact that the x -intercept a has a value of −273.15°C, and it is evident that this value, called absolute zero, corresponds to the temperature at which the volume of a gas extrapolates to zero, its logically limiting value. This condition is the basis of the absolute temperature, or Kelvin scale, and was proposed in the mid-1800s by Lord Kelvin (British physicist William Thomson). Charles's law can be expressed in terms of the absolute temperature as
V = c′T
where c′ is a constant; thus, the volume of a gas is directly proportional to its absolute temperature.
The relationship between the volume of a gas and the quantity of the gaseous material, as represented by the number of moles, was established by Amedeo Avogadro in the early 1800s. He deduced from experiments performed by Joseph-Louis Gay-Lussac that equal volumes of different gases at the same temperature and pressure contained the same number of moles. This idea leads to Avogadro's law, which states that the volume of a gas at constant temperature and pressure is directly proportional to the number of moles of the gas, or
V = c″n
where c″ is a constant.
The three relations, Boyle's, Charles's, and Avogadro's laws, connecting the volume of a gas with its pressure, (absolute) temperature, and mole number, respectively, can be combined into one expression, called the ideal-gas equation of state, or V = nRT/P, in which R is a universal constant, valid for all gases. The value of R is 0.08206 L-atm/mol-K or, in SI units, 8.314 J/mol-K. The ideal-gas equation is usually expressed as
PV = nRT
A gas that obeys this equation is called an ideal or perfect gas. Notice that the identity of the gas is not represented in this equation; in this sense, an ideal gas is hypothetical. The ideal-gas equation works well in the limit of low pressures (where intermolecular interactions are negligible) and/or high temperatures.
There are many other equations of state, such as the van der Waals equation, that are designed to account for gas properties at higher pressures and/or lower temperatures. These equations contain one or more parameters whose values are specific for the gas in question.
Molecular Motion
Beginning with the empirical development of the gas laws, which explained how gases behave, scientists began to seek an understanding of the mechanism of this behavior. By the mid-1800s the work of several scientists, including James Joule, Rudolf Clausius, James Clerk Maxwell, and Ludwig Boltzmann, led to the development of the kinetic-molecular theory (KMT) of gases. This theory employed several assumptions: (1) Gas particles (i.e., atoms or molecules) are point masses—meaning they have negligible volume, (2) they undergo constant random motion involving frequent collisions, (3) attractive and repulsive forces between molecules are negligible, and (4) the average kinetic energy of molecules is proportional to the absolute temperature.
According to this model, pressure is caused by the collisions that molecules make with the walls of its container. An analysis of this molecular motion using Newton's laws leads to an expression identical to the ideal-gas law. An important result of the theory is that the average kinetic energy of one mole of gas can be expressed in terms of the absolute temperature

| COMPOSITION OF GASES IN EARTH'S ATMOSPHERE AT SEA LEVEL IN VOLUME (OR MOLE) PERCENT | |
| Composition | Component (% by Volume) a |
| a Note that percent by volume is equivalent to percent by moles (Avogadro's law) | |
| N 2 , nitrogen | 78.084 |
| O 2 , oxygen | 20.948 |
| Ar, argon | 0.934 |
| CO 2 , carbon dioxide | 0.0345 |
| Ne, neon | 0.00182 |
| He, helium | 0.000524 |
| CH 4 , methane | 0.000168 |
| Kr, krypton | 0.000114 |
| H 2 , hydrogen | 0.00005 |
| Xe, xenon | 0.0000087 |
where M is the molar mass, u its average molecular speed, R the gas constant. The average kinetic energy of a gas depends only on T and is independent of its mass. The root-mean-square speed, u rms , of a gas is equal to
and the KMT predicts that for methane, CH 4 ( M = 0.0160 kg/mol), near room temperature (300 K) u rms = 394 m/s (or 882 miles/hr!). Although this result seems very large, experimental measurements are consistent with this value. Another property obtained from the KMT is the mean free path λ , which is the average distance a molecule travels between collisions. Analysis shows that λ varies inversely with pressure, as well as the size of the molecule, a property not accounted for in simple KMT. For a pure gas,
where d is the molecular diameter. For the oxygen molecule O 2 , d ≈ 2.4 × 10 −10 m, and λ ≈ 1.6 × 10 −7 m at 300 K and 1 atm. Under these conditions, the molecule travels a distance that is about 670 times its diameter before it collides with another molecule.
Earth's Atmosphere
Perhaps the most important and ubiquitous gas is Earth's atmosphere, which is a complex mixture of compounds. The composition of gases in the atmosphere at sea level, excluding water vapor, aerosols, and particulate suspensions, which vary regionally and climatically, is listed in Table 1.
Although carbon dioxide (CO 2 ) is present in trace amounts, it is an exceedingly important constituent. Until about 1800 CO 2 composition was constant at about 0.028 percent. After that time it began to increase, presumably because of the combustion of fossil fuels. In 1900 the CO 2 level was ca. 0.0295 percent; currently it is 0.0345 percent. CO 2 and several other gases, such as methane (CH 4 ) and nitrogen oxides, which are, in part, anthropogenic, are called greenhouse gases because they absorb infrared radiation from Earth that would otherwise be transmitted into space. Thus, these gases, while transmitting visible light from the Sun, essentially retain heat in a way similar to the glass panels of a greenhouse. The apparent trend in global warming has been attributed to the rapid and continuing increase in the atmospheric composition of greenhouse gases observed in the past 50 to 100 years.
SEE ALSO Avogadro, Amedeo ; Air Pollution ; Boltzmann, Ludwig ; Boyle, Robert ; Charles, Jacques ; Gay-Lussac, Joseph-Louis ; Maxwell, James Clerk ; Noble Gases .
Arthur M. Halpern
Bibliography
Jacob, Daniel J. (1999). Introduction to Atmospheric Chemistry. Princeton, NJ: Princeton University Press.
Lide, David R., ed. (2002). CRC Handbook of Chemistry and Physics, 83rd edition. Boca Raton, FL: CRC Press.
Zumdahl, Steven S., and Zumdahl, Susan A. (2000). Chemistry, 5th edition. Boston: Houghton Mifflin, pp. 187–230, 270–271.
Comment about this article, ask questions, or add new information about this topic: