Ct Scans
A computed axial tomograph is an axial (cross sectional) view computed from a large set of values, each corresponding to the attenuation of an x-ray beam passed transversely (i.e. in the plane of the desired image) through the subject. In medical applications the subject is a patient; however, applications are not limited to medicine. Computed tomography (fr Greek tomos and graphikos for section or slice and drawing, respectively) has applications in areas as diverse as material sciences, archeology, manufacturing, and facility security.
A CAT Scanner is a machine designed to collect and process the x ray transmission data required to construct and display a computed axial tomograph. "CT scanner" is nearly synonymous with CAT scanner, but recognizes that computed views are not limited to axial views.
Basic physics
X rays (comprised of photons) diminish exponentially in intensity as they pass through a material of thickness Δx according to the relationship:
(1) I out = I in * e −aΔx . Where "I" is the intensity, "e" is the Naperian constant, "a" is the attenuation coefficient of the material, and "Δx" is the distance traveled. When "n" adjacent materials are transversed, the formula can be applied repeatedly to yield
(2) I out = I in * e −a 0 Δx 0 * e −a 1 Δx 1 * e −a 2 Δx 2 * … * e −a n Δx n . Which is equivalent to
(3) I out = I in * e −a 0 Δx 0 + −a 1 Δx 1 + −a 2 Δx 2 + … + −a n Δx n , which yields
(4) −ln(I out /I in ) = a 0 Δx 0 + a 1 Δx 1 + a 2 Δx 2 + … + a n Δx n
Thus the logarithm of the attenuation along any ray is a linear function of the distances traveled through the materials encountered and their respective attenuation coefficients.
Scope of computation
The fundamental computational problem of axial tomography is to solve a group of equations for the attenuation coefficients of each voxel. A voxel–is a volume element, in particular the smallest volume element the system can manage—similar concept to pixel. The solution grid is chosen from the points where rays from different rotation angles intersect. After the attenuation coefficients have been determined for the solution grid, averaging and interpolation are used to superimpose a display grid of cubical voxels. For useful resolution, voxels must be small, consequently the system of equations
becomes very large, i.e., for a resolution of 2mm x 2mm across a body 500mm (19.7 inches) in diameter the minimum number of equations for a solution will be on the order of 64,000 for each transverse slice or "cut." If the detector arc contains 256 detectorsper slice, recordings from about 250 positions around the axis are required. Scanning a region 10 cm long with a corresponding resolution (2mm/cut) will require 50 cuts and the total number of equations becomes 3,200,000. Fortunately mathematicians and computer scientists have been pursuing efficient computational methods for similar problems for decades. A profound improvement was made in 1965 when J. W. Cooley and J. W. Tukey introduced the fast Fourier transform. Present methods require working knowledge of linear algebra, calculus, differential equations, matrices, vector calculus, Fourier transforms, and some programming experience to be appreciated.
By 2002, scans of the resolution and extent mentioned above could be acquired and solved within a few seconds. Consequently the radiation exposure of the patient was limited to safe levels despite the amount of information obtained.
Practical Scanners
A realistic scanner (Figure 1) has a point as the source of x rays. This point produces a wedge-shaped beam aimed at an arc of detectors (possibly more than one layer thick, to acquire data for adjacent cuts simultaneously). The source and detectors have a constant geometric relationship because they are fixed to a rigid ring (gantry). The ring is rotated about the axis of the subject lying on an x ray–transparent table that moves along the ring axis. Exposures are made at many angular positions to acquire sufficient data to compute the voxel values for the cut(s). For the resulting attenuation data-set to be useful it must be recorded with precise values for the corresponding angular position of the beam and the linear position of the table. If slip rings (or telemetry) connect the power, control, and data cables between the
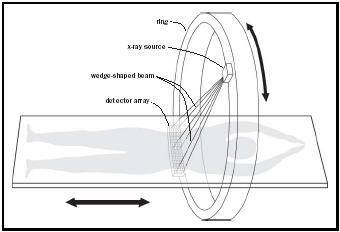
ring and the frame, the ring can rotate continuously without reversing between cuts. Continuous rotation with continuous linear table motion of one detector-array-width per ring-revolution produces an aptly named helical scan (loosely called a "spiral" scan). If the detectors and processing electronics are fast enough, rotation, exposure, and detection can also be continuous. The fastest systems can complete a scan of a beating heart so rapidly that there is negligible motion artifact in the computed image—similar to stop action photography with fast shutter speeds and fast film.
History
Austrian mathematician Johann Radon (1887–1956) suspected that images might be created from rays traveling in the plane of a subject and in 1917 presented a proof that this was at least theoretically possible. Decades later, his work proved fundamental in developing methods for computing axial tomographs. CAT scanners could not be built until the late 1960s, as even a rudimentary CAT scanner requires the confluence of imagination and several technologies (just as da Vinci's helicopter had to wait for the invention of the internal combustion engine and light metal alloys).
CAT scanners require affordable computational power, reliable micro-sized solid state detectors, materials dimensionally stable with respect to time and temperature, high power x ray–source tubes with precisely shaped anodes, and considerable sophistication in computational methods. Similarly, the burgeoning field of computational chemistry would be nonexistent without computational power unattainable until very the end of the twentieth century.
British engineer Sir Godfrey Newbold Hounsfield invented the CAT scanner as soon as it was practical to do so. Beginning in the late 1960s he conceived demonstration conceptual laboratory models that took hours to acquire and analyze data for a single low-resolution slice. Hounsfield was assisted in implementing his ideas by radiologists James Ambrose and
Louis Kreel. Hounsfield obtained a British patent in 1972 and a US patent in 1976 and shared the 1979 Nobel Prize for medicine and physiology, with Allan MacLeod Cormack, a physicist at Yale who had independently developed mathematical methods required to solve the inverse problem of axial tomography.
Refinements
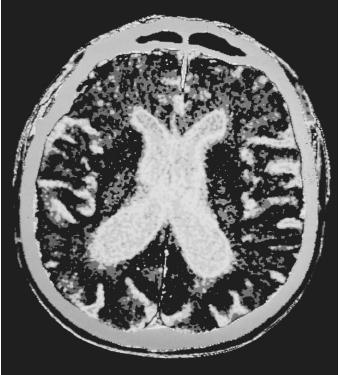
Such a vast quantity of information is collected by high-resolution scanners that additional refinements are needed to help physicians quickly absorb the information. The principal aids are computed color contrasts and images computed from selected viewpoints.
Contrast and Color. The attenuation differences of similar tissues can be enhanced by the administration (intravenously or by mouth) of contrast agents (sometimes called "dyes") that will collect preferentially in one tissue type before eventual elimination by the body. These agents contain salts of heavy atoms, such as iodine, that attenuate x rays more rapidly than living tissue. Even if the attenuation coefficient change might be inapparent to a human viewing a simple gray-level presentation of the data, differences detectable to the imaging system (with or without contrast) permit attenuation coefficients within different ranges to be displayed as different colors: such as red for blood, pink for muscle, silver for tendon, ivory for bone, and yellow for nervous tissue.
Computed Views. By convention, medical CAT views are oriented with the viewer looking from the feet toward the head with the patient supine. However once the grids of multiple slices have been solved for the attenuation coefficient of each voxel, there are no restrictions except imagination and computation costs on how that information can be presented. Such constructed views actually contain no more information than a series-of-slices presentation, but they can present the information in a way that emphasizes clinically important details. Imagine a rash on the inside of the thorax, this would be very difficult to perceive by mentally integrating the subtle chest wall changes from dozens of slice views. In contrast a computed view looking toward the chest wall from inside the thorax might make the rash obvious. However, only a careful medical history and examination would prompt the physician to request that view from the infinite number of possible computed views.
New applications
Very high resolution systems (voxel diameters of 1 mm or less) may replace exploratory procedures such as endoscopy. The scan data can be processed interactively to give the physician views corresponding to a "virtual" endoscopic examination under his control. However, parallel studies in which hundreds of patients receive literal or virtual visualization procedures with comparison of diagnostic accuracy, and long term outcome will be necessary before virtual examinations can be accepted as the standard of medical care.
SEE ALSO Nuclear Magnetic Resonance ; Spectroscopy .
J. Carver Hill
Bibliography
Berland, Lincoln L. (1987). Practical CT - Technology and Techniques. New York: Raven Press.
Byers, Paula K., ed. (1998). Encyclopedia of World Biography. 2nd edition. Detroit: Gale Research.
Castronova, Frank V., ed. (1998). Almanac of Famous People 6th edition. Detroit: Gale Research.
Gillispie, Charles Coulston, ed. (1975). Dictionary of Scientific Biography. New York: Scribner.
Hermon, Gabor T. (1998). Geometry of Digital Spaces. Boston: Birkhäuser.
Juhl, John H., and Crummy, Andrew B. eds., (1987). Paul and Juhl's Essentials of Radiologic Imaging. Philadelphia: Lippincott. pp 1–20.
Kak, Avinash C. and Slaney, Malcom (1988). Principles of Computerized Tomographic Imaging. New York: IEEE Press.
Leon, Steven J. (2002). Linear Algebra with Applications. New Jersey: Prentice Hall.
Sclessinger, Bernard S., and Sclessinger, June H., eds. (1986). The Who's Who of Nobel Prize Winners. Arizona: The Ornyx Press.
Internet Resources
GE Medical Systems. Computed Tomography. Available at http://www.gemedicalsystems.com/rad/ct .
Imaginis. Computed Tomography Imagining (CT Scan, CAT Scan). Available at http://www.imaginis.com/ct-scan .
Information available at http://www.yourmedicalsource.com .
Comment about this article, ask questions, or add new information about this topic: